티스토리 뷰
Machine Learning -Google MLCC 1주차 (ML소개, ML문제로 표현하기, ML로 전환하기)
Ideveloper2 2018. 7. 13. 22:26Machine Learning -1주차
:(ML소개, ML문제로 표현하기, ML로 전환하기 )
| ML 소개
소프트웨어 엔지니어로서 세가지를 잘할 수 있게 된다.
- 1. 먼저 프로그래밍 시간을 줄일 수 있는 도구를 얻게 된다.( 짧은 시간에 더 안정적인 프로그램을 만들수 있다.)
- 2. 제품을 맞춤 설정하여 특정 집단의 사용자에게 더 잘맞는 제품을 제공 할 수 있다.
- 3. 머신러닝을 사용하면 프로그래머로서 수동으로 할 방법이 없어 보이는 문제를 해결할수 있다.
머신러닝은 문제에 관해 생각하는 방법을 바꾼다.
- 수리과학에서 자연과학으로 초점이 바뀐다.
- 불확실한 세계를 관찰하고 실험을 하고 논리가 아닌 통계를 사용하여 실험 결과를 분석한다.
| ML 문제로 표현하기
(지도) 머신러닝
ML 시스템은 입력을 결합해 이전에 본 적없는 데이터를 적절히 예측하는 방법을 학습한다.
라벨
라벨은 예측하는 항목(단순 선형 회귀의 y 변수)
ex) 밀의 향후 가격, 사진에 표시되는 동물의 종류, 오디오 클립의 의미 ...
특성
입력변수(단순 선형 회귀의 x 변수) 간단한 머신러닝 프로젝트에선 특성 하나를 사용, 복잡한 프로젝트는 수백만개 특성 사용
스팸 감지 예에는 다음과 같은 특성이 포함될 수 있다.
- 이메일 텍스트의 단어
- 보내는 사람의 주소
- 이메일이 전송된 시간
- '이상한 속임수 하나'라는 구문이 포함된 이메일
- 라벨이 있는 예
- 라벨이 없는 예
라벨이 있는 예에는 특성과 라벨이 모두 포함된다. 즉 다음과 같다.
labeled examples: {features, label}: (x, y)예를 들어 다음 표에는 캘리포니아 주택 가격 정보가 포함된 데이터 세트 에서 추출한 라벨이 있는 예 5개가 표시된다.
| housingMedianAge 특성 | totalRooms 특성 | totalBedrooms 특성 | medianHouseValue 특성 |
|---|---|---|---|
| 15 | 5612 | 1283 | 66900 |
| 19 | 7650 | 1901 | 80100 |
| 17 | 720 | 174 | 85700 |
| 14 | 1501 | 337 | 73400 |
| 20 | 1454 | 326 | 65500 |
라벨이 없는 예에는 특성은 포함되지만 라벨은 포함되지 않습니다. 즉 다음과 같습니다.
unlabeled examples: {features, ?}: (x, ?)
라벨이 있는 예로 모델을 학습시킨 다음 해당 모델을 사용하여 라벨이 없는 예의 라벨을 예측한다. 스팸 감지 예에서 라벨이 없는 예는 사람이 라벨을 지정하지 않은 새 이메일이다.
정리: 라벨이 있는 예로 모델을 학습 후 라벨이 없는 예의 라벨을 예측
모델 수명의 두단계1. 학습: 모델을 만들거나 배우는것. 라벨이 있는 예를 모델에보여주고, 모델이 특성과 라벨의 관계를 점차적으로 학습하도록 함.2. 추론: 학습된 모델을 라벨이 없는 예에 적용하는 것을 의미, 학습된 모델을 사용하여 유용한 예측(y or 라벨)을 해냄, 추론하는동안 라벨이 없는 새로운 예로 위 표에서의 medianHouseValue 예측
회귀와 분류
회귀 모델은 연속적인 값을 예측한다.
회귀 모델
- 캘리포니아 주택 가격은 얼마?
- 사용자가 이 광고를 클릭할 확률이 얼마?
분류 모델
- 분류 모델은 불연속적인 값을 예측.
- 주어진 이메일 메시지가 스팸인가, 아닌가
- 이 이미지가 강아지, 고양이, 햄스터의 이미지 인가
지도 학습
- '스팸' 또는 '스팸 아님'으로 표시되지 않은 이메일은 라벨이 없는 예이다. 라벨이 '스팸' 및 '스팸 아님' 값으로 구성되므로 아직 스팸 또는 스팸 아님으로 표시되지 않은 이메일은 모두 라벨이 없는 예이다.
- 일부 라벨은 신뢰할 수 없을 수도 있다. 확실히 이 데이터 세트의 라벨은 특정 이메일 메시지를 스팸으로 표시하는 이메일 사용자로부터 가져온 것일 수도 있다. 의심스러운 모든 이메일 메시지를 스팸으로 표시하는 사용자는 아주 적기 때문에 특정 이메일이 스팸인지 확인하기 어려울 수도 있다. 또한 일부 스팸 발송자나 봇넷은 결함이 있는 라벨을 제공하여 모델을 고의적으로 손상시킬 수 있다.
특성 및 라벨
- 사용자의 신발 설명 클릭수는 유용한 라벨이다. 사용자는 마음에 드는 신발의 설명만 읽으려 할 것이다. 따라서 사용자 클릭수는 좋은 학습 라벨로 사용할 수 있는 관찰 가능하고 수량화 가능한 측정항목이다.
- 신발 크기는 유용한 특성이다. 신발 크기는 추천된 신발이 사용자의 마음에 들 것인지 쉽게 확인할 수 있는 수량화 가능한 신호이다. 예를 들어 철수의 신발 크기가 270cm인 경우 모델은 260cm 신발을 추천하면 안 된다.
| ML로 전환하기
아래 내용은 구글 머신러닝 단기과정 내용을 대부분 발췌함.
선형회귀
그림 1. 1분당 우는 횟수 및 섭씨온도
귀뚜라미가 우는 횟수가 증가할수록 온도증가
우는 횟수와 온도는 선형 관계, 위 관계를 근사치로 한 아래의 직선
그림 2. 선형 관계
모든 점을 완벽하게 통과하지는 않지만, 선은 우리에게 있는 온도 데이터와 우는 소리 데이터의 관계를 명확히 보여준다.
대수학을 약간 적용하면 이 관계를 다음과 같이 작성할 수 있다.
여기서
- 는 섭씨온도, 즉 예측하려는 값.
- 은 선의 기울기.
- 는 1분당 우는 횟수, 즉 입력 특성 값.
- 는 y절편.
머신러닝 에서의 모델 방식은 아래와 같다.
여기서
- 는 예측된 라벨(얻고자 하는 출력)
- 는 편향(y절편)이다. 일부 머신러닝 자료에서는 (w_0\)이라고도 함.
- 은 특성 1의 가중치이다. 가중치는 위에서 으로 표현된 '기울기'와 같은 개념.
- 은 특성(알려진 입력)이다.
새로운 분당 우는 횟수에서 온도를 추론(예측)하려면 값을 이 모델에 삽입하기만 하면 된다.
아래 첨자(예: , )는 여러 특성에 의존하는 좀 더 정교한 모델을 예시합니다. 예를 들어 세 가지 특성에 의존하는 모델은 다음과 같은 방정식을 사용.
학습 및 손실
모델을 학습?
:라벨이 있는 데이터로부터 올바른 가중치와 편향값을 학습(결정)하는 것.
지도 학습에서 머신러닝 알고리즘은 다양한 예를 검토하고 손실을 최소화 하는 모델을 찾아봄으로써 모델을 만들어냄 -> 이 과정을 경험적 위험 최소화라고 함.
손실?
:잘못된 예측에 대한 벌점
즉, 손실은 한 가지 예에서 모델의 예측이 얼마나 잘못되었는지를 나타내는 수이다. 모델의 예측이 완벽하면 손실은 0이고 그렇지 않으면 손실은 그보다 커진다.
모델 학습의 목표는 모든 예에서 평균적으로 작은 손실을 갖는 가중치와 편향의 집합을 찾는 것이다.
예를 들어 그림 3에서 왼쪽은 손실이 큰 모델이고 오른쪽은 손실이 작은 모델이다.
- 빨간색 화살표는 손실
- 파란색 직선은 예측
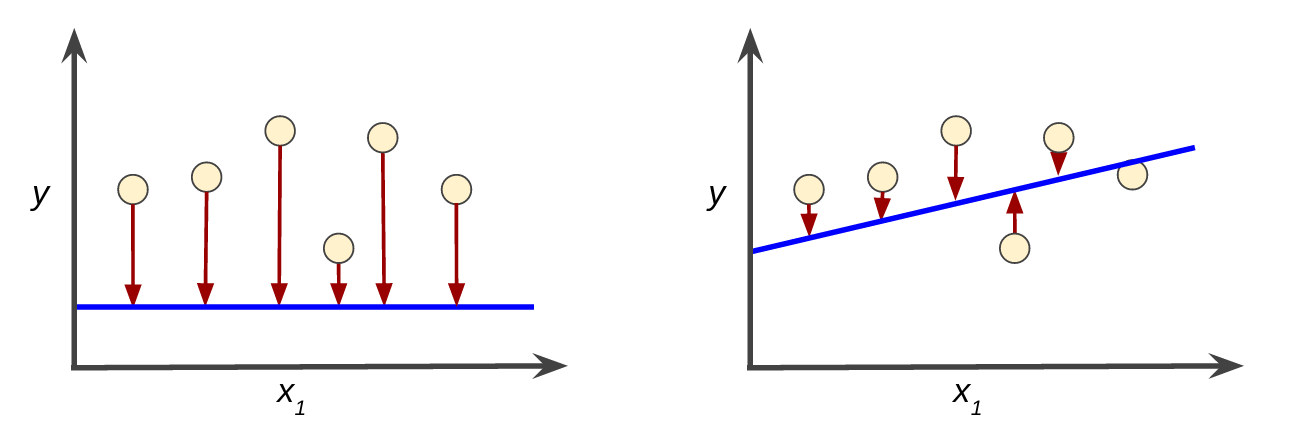
그림 3. 왼쪽 모델은 손실이 크고 오른쪽 모델은 손실이 작음
오른쪽 그래프의 파란색 직선 -> 왼쪽 그래프의 파란색 직선보다 훨씬 더 예측을 잘 하는 모델 (손실이 적기 떄문)
제곱 손실: 잘 알려진 손실 함수
여기에서 살펴볼 선형 회귀 모델에서는 제곱 손실(또는 L2 손실)이라는 손실 함수를 사용한다. 데이터 하나의 제곱 손실은 다음과 같이 나타낸다.
= the square of the difference between the label and the prediction = (observation - prediction(x))2 = (y - y')2
평균 제곱 오차(MSE)는 예시당 평균 제곱 손실. MSE를 계산하려면 개별 예의 모든 제곱 손실을 합한 다음 예의 수로 나눈다.
여기서
는 예이며, 다음과 같다.
- 는 모델이 예측하는 데 사용하는 특성 집합(예: 온도, 나이, 짝짓기 성공률).
- 는 예의 라벨(예: 분당 우는 소리).
- 은 특성 집합과 결합된 가중치 및 편향의 함수. -> 위 그래프에서 파란색
- 는 쌍과 같이 여러 라벨이 있는 예가 포함된 데이터 세트. -> 위 그래프에서 노란색 점들
- 은 에 포함된 예의 수.
MSE는 머신러닝에서 흔히 사용되지만, 모든 상황에서 최선인 유일한 손실 함수.
내 생각: 그렇다면 최소한의 손실을 도출해내는 손실 함수를 모델링 하는것이 최종적 목표일까?
'AI > Machine Learning' 카테고리의 다른 글
| Machine Learning - 특성교차, 정규화:단순성 (1) | 2018.07.21 |
|---|---|
| Machine Learning -Google MLCC 1주차 (일반화: 과적합의 위험, 데이터 분할) (0) | 2018.07.15 |
| Machine Learning - Google MLCC 1주차 (손실줄이기) (0) | 2018.07.15 |
